[Toán rời rạc/Chương V] Bài toán đếm

CHƯƠNG V: BÀI TOÁN ĐẾM

I, Quy tắc cơ bản của Counting (Đếm)

* Quy tắc nhân: Giả sử, có 1 quy trình có thể được chia thành một chuỗi gồm 2 việc. Nếu có \(n_1\) cách để thực hiện việc đầu tiên và có \(n_2\) cách để thực hiện việc thứ 2 thì có tổng cộng \(n_1.n_2\) cách để thực hiện quy trình này

Ví dụ: Có 2 người và 10 viên bi khác nhau. Có bao nhiêu cách chọn bi để 2 người nhận được viên bi khác nhau

Ta có: Người đầu tiên có 10 cách chọn bi, do để 2 người có viên bi khác nhau thì sau khi người thứ nhất chọn thì còn 9 cách chọn bi (trừ đi 1 viên của người đầu) \(\Rightarrow\) Có tổng cộng 9.10 = 90 (cách)

* Counting ánh xạ:

Ví dụ: Cho 2 tập hợp A và B, tập A có m phần tử và tập B có n phần tử. Hỏi có bao nhiêu ánh xạ

Ta có: Mỗi phần tử trong A đều có thể ánh xạ đến n phần tử trong B, tức là 1 phần tử thì có n (cách), 2 phần tử thì là n.n (cách), 3 phần tử là n.n.n (cách)...

\(\Rightarrow\) Với m phần tử trong A thì: \(n^m\) (cách) ánh xạ đến n phần tử trong B

* Counting trong đơn ánh (One-to-One):

- Đơn ánh là 2 phần tử khác nhau trong A thì ánh xạ đến 2 phần tử khác nhau trong B (Phần tử trong tập A \(\leq\) phần tử trong tập B)

- Nếu phần tử trong tập A \(\geq\) phần tử trong tập B thì không có đơn ánh

Ví dụ 1: Tập A có 3 phần tử, tập B có 5 phần tử. Hỏi có bao nhiêu cách đơn ánh từ tập A sang tập B

Ta có: 5.4.3 = 60 (cách)

Ví dụ 2: Tập A có 5 phần tử, tập B có 3 phần tử. Hỏi có bao nhiêu cách đơn ánh từ tập A sang tập B

Do số phần tử tập A lớn hơn tập B, điều này có nghĩa là có thể có các phần tử khác nhau thuộc A nhưng cho ra ánh xạ cùng nhau thuộc B

\(\Rightarrow\) Vi phạm quy tắc đơn ánh \(\Rightarrow\) Không có cách nào

* Counting tập con trong tập vô hạn:

- Số tập con khác nhau trong tập vô hạn S là \(2^{|S|}\)

* Quy tắc cộng (Nguyên tắc bao gồm - loại trừ) (Inclusion-Exclusion)

- Cho A và B là 2 tập hợp rời rạc (disjoint sets) 

            thì, | A \(\cup\) B | = |A| + |B|

- Cho A và B là 2 tập hợp ngẫu nhiên (arbitrary sets)

            thì, | A\(\cup\) B | = |A| + |B| - | A \(\cap\) B |

Ví dụ: Có bao nhiêu chuỗi bit có độ dài là 8 hoặc bắt đầu là bit 1 hoặc kết thúc là 2 bit 0?

Ta có: Số chuỗi bit bắt đầu bằng bit 1 là: \(2^7\) (chuỗi)

           Số chuỗi bit kết thúc bằng 2 bit 0 là: \(2^6\) (chuỗi)

           Số chuỗi bit vừa bắt đầu bằng bit 1, vừa kết thúc bằng 2 bit 0 là: \(2^5\) (cách)

\(\Rightarrow\) Số chuỗi bit hoặc bắt đầu bằng 1, hoặc kết thúc bằng 2 bit 0 là \(2^7 + 2^6 - 2^5 = 160\) (chuỗi) 

* Counting số phần tử chia hết

- Số các số nguyên dương không vượt quá n (not exceeding n) và chia hết cho k là \(\lfloor \frac{n}{k} \rfloor\)

Ví dụ: Số các số nguyên dương không vượt quá 1000 và chia hết cho 12 là?

Ta có:  \(\lfloor \frac{1000}{12} \rfloor\) = 83 (số)

* Các vấn đề phức tạp hơn của bài toán đếm

- Cho \(A_1, A_2,...,A_m\) với m tập hợp. Giả sử \(A_i \cap A_j = \emptyset\) với i, j = 1, 2,..., m và \(i \neq j\), thì:

          | \(A_1 \cup A_2 \cup \cdots \cup A_m\) | = |\(A_1\)| + |\(A_2\)| + ... + |\(A_m\)|

* Quy tắc chia:

- Giả sử tập hữu hạn A là hợp của n tập con rời rạc từng cặp, mỗi tập con có d phần tử thì: \(n = \frac{|A|}{d}\)

Ví dụ: Có bao nhiêu cách xếp 4 người vào chiếc bàn tròn sao cho chỗ ngồi được coi là giống nhau khi mỗi người có cùng 1 người bên trái và cùng 1 người bên phải?

Ta có tổng số cách xếp là 4! = 24 (cách) nhưng để loại các trường hợp ngồi giống nhau thì ta lấy \(\frac{24}{4} = 6\) \(\Rightarrow\) Có 6 (cách)

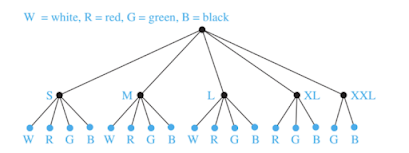
* Sơ đồ cây (Tree diagrams)

- Ta dùng sơ đồ cây để tiện cho việc chia trường hợp  

Ví dụ: Chia tập hợp các màu áo theo size 

* Hoán vị (Permutation)

- 1 hoán vị của của 1 tập hợp là sự sắp xếp của các đối tượng trong tập hợp. Một sự sắp xếp có thứ tự của n phần tử của một tập hợp được gọi là 1 hoán vị n.

Ví dụ: Có bao nhiêu hoán vị để trong chuỗi ABCDEFGH chứa chuỗi ABC?

Ta coi chuỗi ABC là 1 đối tượng, và 5 đối tượng khác là D, E, F, G, H

\(\Rightarrow\) Số hoán vị chứa phần tử ABC liền nhau là: 6! = 6.5.4.3.2.1 = 720

* Tổ hợp (Combinations)

- Các phần tử ngẫu nhiên không có thứ tự trong tập hợp

- Công thức: C(n,r) = \(\frac{n!}{r!(n-r)!}\)

* Tổ hợp với sự lặp lại (Combinations with Repetition)

- Định lý: Số lượng các hoán vị r của 1 tập hợp n đối tượng với sự lặp lại là \(n^r\)

- Định lý: Có C(n + r - 1, r) = C(n + r - 1, n - 1), tổ hợp r từ một tập hợp có n phần tử khi lặp lại 

* Chia để trị (Divide and conquer)

- Cho f(n) là một hàm tập hợp các số nguyên. Một quan hệ chia để trị cho f có dạng:

            f(n) = a.f(\(\frac{n}{b}\)) + g(n); với g(n) là 1 hàm nào đó; a, b là số thực 

P/s: Bài tập và tài liệu nghiên cứu thêm (nếu cần) được tổng hợp ở link dưới sau:

https://drive.google.com/drive/folders/1prjWpIKCWabo4INEDkQO86Z0WYWqMJks?usp=sharing